Generatore di Cockcroft-Walton

Generatore di Cockcroft-Walton.

Dizionari Enciclopedia Storia Link utili Down

Cockcroft-Walton, Generatore di.

S'indica con questo nome una macchina elettrica destinata alla produzione di elevatissime tensioni, realizzata per la prima volta nel 1932 da J. Cockcroft ed E.T. Walton e divenuta poi di uso alquanto comune. Per la loro invenzione questi due ricercatori ottennero nel 1951 il premio Nobel per la fisica. Il generatore di Cockcroft e Walton è sostanzialmente un moltiplicatore di tensione. Esso viene alimentato con una tensione alternata ad una frequenza opportuna, fornita da un trasformatore o da un generatore, e dà come uscita una tensione variabile, generalmente pulsante, di valore molto elevato. Comunemente si costruiscono generatori di questo tipo da qualche decina di kV (1 kV = 1 kilo-Volt = 1.000 Volt); i più grandi raggiungono anche qualche MV (1 MV = 1 mega-Volt = 1.000.000 di Volt). Il principio applicato per elevare la tensione è quello dei moltiplicatori di tensione, che sono circuiti molto semplici, un esempio dei quali è dato in figura. Si è riportato un duplicatore di tensione, cioè un circuito che dà una tensione d'uscita v_u circa doppia della tensione di ingresso v_i vi sono anche dei circuiti triplicatori, quadruplicatori, ecc. di tensione. Dato un duplicatore, basta aggiungere un diodo e un condensatore per ottenere un triplicatore; aggiungendo un ulteriore diodo e condensatore si ha un quadruplicatore, e così via. In teoria si potrebbe continuare all'infinito; in pratica però, man mano che si aggiungono stadi, il guadagno per stadio diminuisce e quindi ad un certo punto l'aggiunta di altri stadi non conviene più. Piuttosto si preferisce porre un altro stadio moltiplicatore in serie al primo, e continuare in questo modo. Il problema principale che si deve affrontare nella costruzione di queste macchine è l'isolamento; non si hanno invece grandi problemi per l'intensità di corrente, dato che si trattano correnti dell'ordine dei milliampère (abbreviato mA: 1 mA = 0,001 Ampère). Nelle prime macchine gli elettrodi erano in aria e quindi le dimensioni della macchina stessa erano dettate dalla tensione raggiunta. Dato che la tensione di perforazione dell'aria a pressione atmosferica e temperatura ambiente, con umidità non troppo elevata, è dell'ordine di 1 MV/metro, è necessario che fra due punti della macchina che si trovano a differenza di potenziale di 1 MV si abbia una distanza di almeno un metro. Anche oggi i più grandi generatori di questo tipo sono costruiti con isolamento in aria e possono avere un'altezza di 10÷15 metri. Per costruire generatori più compatti si ricorre all'artificio di racchiudere in un'atmosfera opportuna (ad es. azoto e anidride carbonica) sotto pressione (5÷15 atmosfere) le parti ad alta tensione; la tensione di perforazione dei dielettrici gassosi dipende infatti dalla natura delle molecole del gas e dalla sua densità, che cresce con la pressione. Questo sistema richiede però l'uso di un contenitore a pressione, cosa che può anche non essere conveniente in quelle applicazioni in cui non si hanno restrizioni di spazio. Il generatore di Cockcroft-Walton può avere diversi usi; il primo, che ancor oggi è il più importante, è come acceleratore elettrostatico (V. ACCELERATORE DI PARTICELLE), onde si parla spesso di acceleratore di Cockcroft-Walton.

Linea flashing backefro

Questo non è altro che un generatore come quello sopra descritto applicato all'alimentazione di un tubo a vuoto ad un'estremità del quale si trova un generatore di particelle, mentre all'altra si trova un bersaglio. Si possono ottenere fasci diretti di particelle cariche (elettroni, protoni, positoni, elioni, ioni pesanti, ecc.) sia fasci indiretti (ottenuti per emissione secondaria dal bersaglio) di raggi X, raggi 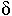Raggi , neutroni, e così via. Da questo punto di vista il generatore di Cockcroft e Walton trova una diffusione notevole come sorgente di particelle già accelerate con una buona energia per gli altri acceleratori di particelle, sia di tipo lineare che circolare. Nella costruzione in recipiente a pressione si possono infatti avere dei generatori di questo tipo in grado di fornire qualche centinaio di kV che hanno dimensioni molto ridotte (ad es. dell'ordine del metro cubo di volume). Questo fa si che si possano facilmente inserire nelle macchine acceleratrici; ad esempio il protosincrotrone da 28 GeV del CERN di Ginevra è alimentato con un acceleratore di Cockcroft-Walton che fornisce protoni a 500 keV di energia e che a sua volta alimenta un acceleratore lineare nel quale le particelle sono portate a 50 MeV prima di essere iniettate nella camera vera e propria del protosincrotrone. Per la sua semplicità, il generatore di Cockcroft e Walton ha avuto numerose applicazioni pratiche anche fuori dall'accelerazione di particelle. Ad esempio grandi generatori di questo tipo sono utilizzati da molti istituti di ricerca e anche da industrie per avere a disposizione delle tensioni assai elevate, ad es. per prove sugli isolanti destinati alle reti elettriche di distribuzione in alta tensione. Sotto forma di acceleratore, la macchina di Cockcroft-Walton è utilizzata in molti campi, dalla produzione di radioisotopi alla sterilizzazione di alimenti o prodotti farmaceutici, all'analisi chimica per attivazione, nei quali si ha necessità di un fascio di particelle ad energia relativamente bassa ma con un costo d'impianto modesto.